X. Princip relativity v prostoročasu
Vždy stojí za to pro analýzu vybrat co nejjednodušší model. Proto naše úvahy začneme od jednorozměrného prostoru, který si můžeme představit ve formě přímky p, ve kterém máme nehybného pozorovatele O. Jestliže přidáme čas jako přímku t kolmou k prostoru p, dostaneme dvourozměrný prostoročas (obr. 8).
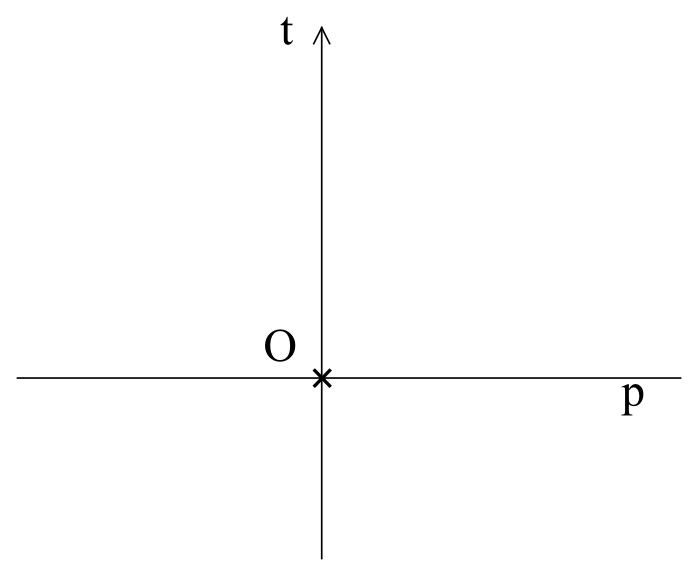
Obrázek 8
Předpokládáme, že náš pozorovatel se nepohybuje v prostoru (nebo přesněji: nepohybuje se vzhledem k systému souřadnic, který je s ním spojen), to znamená že v prostoročasu se bude pohybovat pouze ve směru osy t a v následujících okamžicích t1, t2, t3 se bude nacházet v bodech t1, t2, t3 na ose t (obr. 9).
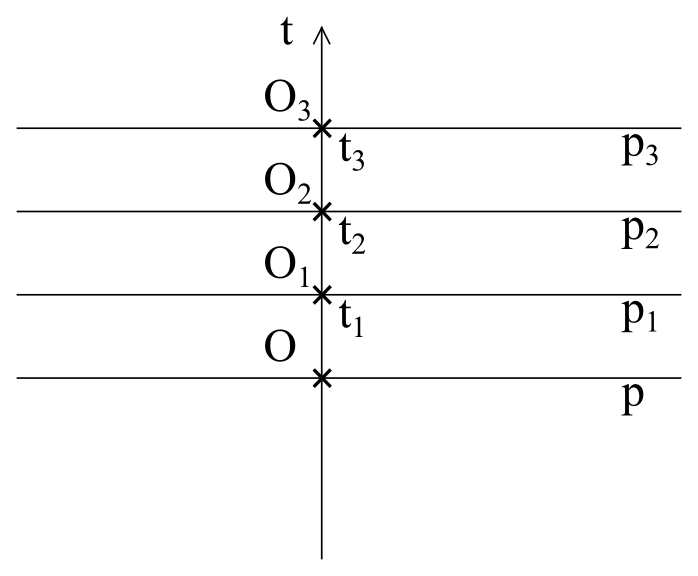
Obrázek 9
Přidejme do našeho modelu ještě jednoho pozorovatele P, který se bude od pozorovatele O vzdalovat rovnoměrným přímočarým pohybem. Jeho dráha v prostoročasu bude mít tvar přímky nakloněné vzhledem časové ose pozorovatele O pod jistým úhlem, jehož velikost bude závislá na rychlosti, jakou se pozorovatel P vzdaluje od pozorovatele O (obr. 10).
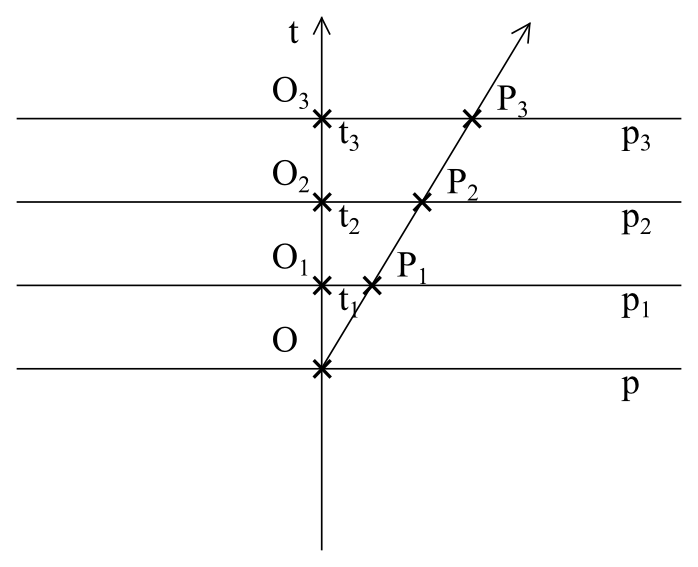
Obrázek 10
Princip relativity nám říká, že pohyb je relativní. Jestliže máme dva pozorovatele, kteří se od sebe vzdalují, není možné určit, kdo je v klidu a kdo se pohybuje. To znamená, že pozorovatel P může tvrdit, že to on je v klidu a nepohybuje se v prostoru a že pozorovatel O se od něj vzdaluje. Pro něj čas plyne ve směru jeho pohybu v prostoročasu, to znamená podél přímky u a prostor pro něj probíhá ve směru přímky r (obrázek 11).
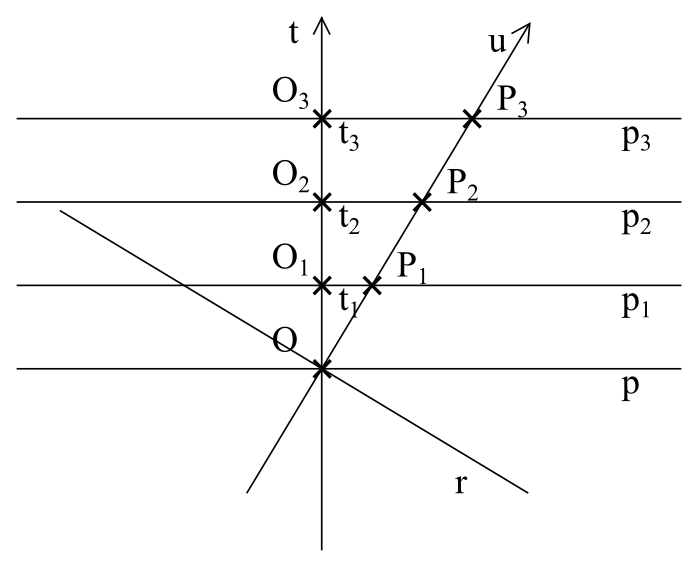
Obrázek 11
Pokud se budeme držet principu relativity, pak situace pozorovatele O i pozorovatele P musí být analogická.
Vzhledem k tomu, že celou operaci můžeme opakovat počínaje pozorovatelem P a rychlost vzdalování se náledujícího pozorovatele můžeme měnit, zdá se, že v našem prostoročase může prostor i čas probíhat libovolným směrem. Protože světlo se musí pohybovat stejně pro každého pozorovatele, znamená to, že se šíří stejnou rychlostí všemi směry prostoročasu a že pro světlo neexistuje čas.
Hned je ale vidět několik problémů. Například co to vlastně je rychlost světla, jestliže pro světlo neplyne čas a celý prostoročas pro něj znamená jenom prostor. Anebo ješte závažnější problém týkající se příčinnosti. Jestliže směr času v prostoročasu může být libovolný, pak se může stát, že pro dva různé pozorovatele může plynout v opačném směru. To by ovšem porušovalo kauzalitu. Tady se musíme v našich úvahách zastavit a promyslet, kde může být chyba a které naše předpoklady musíme změnit.
Často je těžké najít řešení z toho důvodu, že některé předpoklady přijímáme nevědomky. Jsme naučeni a přivyklí na určité názory a vůbec o nich neuvažujeme jako o předpokladech. Takže není snadné přijít s nápadem, že problém s kauzalitou může být způsoben tím, že píšeme a kreslíme na plochém listu papíru a v důsledku toho je náš model plochý. Jenomže jestli není plochý, tak jaký? První nápad je, že rovinu začneme ohýbat a uděláme z ní povrch koule. Jenomže koule nejenže problém neřeší, ale ještě vytvoří další: co se stane, jestliže pozorovatel oběhne celou kouli v čase a vrátí se do místa, ze kterého vyšel? Všechny tyto problémy zmizí, jestliže se koule začne rozpínat. Získáme úplně jinou představu o čase. Čas tu má dva rozměry. Lokální čas, který je pro každého pozorovatele jiný a jeho směr v prostoročasu závisí na rychlosti a čas kosmický ve směru rozšiřování se vesmíru, který je v daném místě stejný pro všechny pozorovatele a týká se i světla. V takovém modelu není narušena zásada kauzality, protože i v případě, že lokální čas dvou pozorovatelů běží v opačném směru, čas kosmický zajistí, že sled událostí je zachován.

